GOOD DAY TO CODE: 4월 2016

2016년 4월 27일 수요일

알고리즘

완전 탐색(Exhaustive Search)

가능한 경우를 모두 구해서 문제의 해결 방법을 찾는 것
실행시간이 너무 길어 제한 시간 내에 문제를 해결할 수 없는 경우가 많다
Brute-force search

N 중 반복문을 이용하는 방법
큐를 이용하는 방법
순열을 이용하는 방법 (재귀 호출로 가능)
재귀 호출을 이용하는 방법

완전 탐색을 구현하기 용이
다른 여러 알고리즘에서 사용
코드가 간결하고 구현이 직관적임

특징: 쉬운 문제를 어렵게 풀어야 한다
특징: 어려운 문제를 쉽게 풀 수 있다
설계

1. 문제해결을 위해 수행해야 하는 작업을
2. 유사한 형태의 여러 조각으로 쪼갠다
3. 그 중 한 조각을 수행
4. 나머지는 자기 자신을 호출해서 해결
5. 기저사례(base case)를 재귀 함수에 추가

기저 사례(base case)

더 이상 쪼갤 수 없는 마지막 조각에 도달한 경우
재귀 호출을 종료하는 조건

예: 1 부터 N 까지의 합, f(n) = f(n-1) + n;

탐색 공간의 배제

전체 탐색 알고리즘을 구현하는 데 있어서 더 이상 탐색하지 않더라도 해를 구하는데 문제가 없는 부분을 판단하여 이 부분에 대해서 탐색을 하지 않도록 하여 탐색의 효율을 높이고자 하는 방법

수학적 배제

이분탐색 알고리즘
수학적으로 공간을 배제해 가는 이 방법은 일종의 탐욕법(greedy)

경험적 배제

처음 시작은 전체탐색과 마찬가지로 해가 될 수 있는 모든 공간을 탐색해 간다. 차이점은 특정 조건을 두고, 이 조건을 기준으로 다음 상태를 계속 탐색할지의 여부를 결정
특정 조건이란 더 이상 탐색하더라도 해를 구할 수 없음을 판단할 수 있는 조건을 말한다
알고리즘이 시작될 때는 이 조건을 설정할 수 없고, 탐색을 진행하는 중에 조건을 설정하고, 상황에 따라서 조건이 갱신된다. 탐색한 정보, 즉 경험한 정보를 이용해서 배제할 조건을 정하기 때문에 경험적 배제라고 한다
일반적으로 가지치기(branch & bound)라고 한다
어떤 조건에 의해서 더 탐색할 공간이 있음에도 불구하고 돌아오는 흐름을 바운딩(bounding) 혹은 커팅(cutting)이라고 한다

구조적 배제

해결 전략에 따른 구현법

백트래킹(Backtracking)

주어진 답이 나올 때까지 검색하다가 중간에 확실히 이 방향이 아니면 다시 이전 상태로 돌아가서 경로를 찾아보는 방법
검색에 제한을 걸 수 있는 조건이 문제에 주어져야 함
특정 알고리즘이 아닌 문제를 해결하는 하나의 방법
가지치기(Pruning) 이라는 방법으로 경우의 수를 줄인다
재귀(DFS), 큐(BFS)

분할정복(Divide and Conquer)

주어진 문제를 더 작은 문제로 나누어 푸는 방법
문제를 더 이상 나누지 않고 풀 수 있을 때까지 나눈다
부분문제의 답을 이용하여 원래 문제의 답을 구한다

DP 와의 차이점은 중복 호출을 하지 않는다

DP 는 중복호출이 일어나 Memoization 을 필요로 하는 경우를 말한다

요소: 분할(divide) / 병합(merge) / 기저 케이스(base case)
루프, 재귀
병합 정렬(Merge Sort)

구현하기 쉬운 대표적인 정렬
최악의 경우에도 O(NlgN) 복잡도
N만큼의 버퍼공간이 추가로 필요

병합용도

분할 정복으로 구현

분할 정복 문제는 어떻게 함수를 만들어야 할지 결정해야 한다

함수->문제를 푸는함수

작은 문제를 어떻게 호출해야 할지 결정

부분 문제의 정답을 합쳐야 하는 경우에는 합치는 것을 어떻게 해야 할지 결정

이진탐색

정렬된 구조에서 목적값의 위치를 찾는 방법
탐색 범위를 반으로 줄여가면서 찾는다
분할 정복의 한 갈래

N/2 로 쪼개 둘 중 하나만 호출한다

DFS (2차원 좌표계에서 DFS 하기)

2차원 좌표로 주어졌을 때 DFS를 하는 경우

지도, 미로, 체스판, 장기 등

임의의 좌표(x, y)에서 상하좌우로 이동가능하다면

배열에서 dx, dy 처리하기 방식으로 총 4 번의 재귀호출

특정 좌표까지 경우의 수라든지 도달 여부 등을 확인할 때 사용 가능
최단거리 문제에서는 부적절함 (시간 초과 발생)

최적화 문제(Optimization Problem)

문제의 답이 하나가 아니라 여러 개이고, 그 중에서 어떤 기준에 따라 가장 '좋은' 답을 찾아 내는 문제들
해결하기 위한 여러 방법들 중에서 가장 기초적인 것이 완전 탐색

시간 안에 답을 구할 수 있는지 확인하는 것이 먼저
문제의 특성을 이용해 단순화할 필요가 있다

가장 유명한 문제

여행하는 외판원 문제(Traveling Sales-man Problem, TSP)

이분탐색

일반적으로 최솟값의 최대화, 최댓값의 최소화 등의 문제에 이용할 수 있는 경우가 많다
일반적으로 최적화 문제를 결정 문제로 바꿔서 생각
결정 문제의 참/거짓의 결과를 이용하여 이분탐색으로 가장 최적의 해를 탐색하는 방법으로 해를 구한다
Binary Search

정렬되어 있는 리스트에서 어떤 값을 빠르게 찾는 알고리즘
리스트의 크기를 N 이라고 할 때 lgN 의 시간이 필요 (절반으로 나누기 때문)

Merge Sort

N 개를 정렬하는 경우

N개를 N/2, N/2 개로 나누고
왼쪽과 오른쪽을 정렬하고
두 정렬한 결과를 하나로 합친다

다이나믹 프로그래밍(Dynamic Programming)

DP, 동적 계획법

Overlapping Subproblem

큰 문제와 작은 문제를 같은 방법으로 풀 수 있다
문제를 작은 문제로 쪼갤 수 있다

Optimal Substructure

문제의 정답을 작은 문제의 정답에서 구할 수 있다

두 번 이상 반복 계산되는 부분 문제들의 답을 미리 저장함으로써 속도의 향상을 꾀하는 알고리즘 설계 기법
기본 전략은 문제를 작은 부분 문제로 나누는 것에서 부터 시작한다
작은 부분 문제를 해결한 결과로 큰 문제를 해결할 수 있다
특징은 중복되는 부분 문제들이 있다는 것
적용 방법

문제를 더 작은 부분 문제로 나눈다
중복되는 작은 부분 문제는 한 번만 계산해서 그 결과를 저장
중복되는 작은 부분 문제들은 여러 번 계산하지 않고 저장한 값을 이용

메모이제이션(memoization)

예) 재귀 함수 + 메모이제이션

같은 입력에 대해 결과가 항상 같아야 한다
같은 입력의 재귀 함수가 (매우 많이) 중복해서 호출된다
예, 피보나치 수

구현 방법

재귀 호출을 이용하는 방법

Top Down
문제를 작은 문제로 쪼개고, 그 중 한 조각을 해결한 다음 나머지 작은 문제를 같은 방법으로 해결한다
장단점

구현이 직관적이고 이해하기 쉽다
전체 부분 문제 중 일부의 답만 필요할 경우 더 빠르게 동작한다
Sliding window 를 사용할 수 없다
스택 오버플로우를 조심해야 한다

Code pattern (문제해결전략 참조)

반복문을 이용하는 방법

Bottom Up
문제 해결에 필요한 가장 작은 문제를 해결하고, 문제를 조금씩 크게 만들어 가면서 해결한다
장단점

구현이 대개 더 짧다
재귀 호출 보다 조금 더 빠르다
Sliding window 를 사용할 수 있다
구현이 비직관적이고, 이해하기 어렵다
부분 문제들을 해결하는 순서에 신경을 써야 한다

가장 유명한 예는 이항 계수(binomial coefficient)의 계산

이항 계수 C(n, r) 는 n 개의 서로 다른 원소 중에 r 개의 원소를 순서 없이 골라내는 방법의 수를 나타내는 것

점화식: C(n, k) = C(n - 1, k - 1) + C(n-1, k)

함수의 반환 값이 그 입력 값만으로 결정되는 참조적 투명 함수(referential transparent function)의 경우에만 메모이제이션이 적용가능하다

그래프

대상(object)사이의 관계(relation)를 나타내는 자료구조
대상 -> 정점(Vertex or node)
관계 -> 간선(Edge)
인접(Adjacent)

간선으로 연결되어 있는 두 정점을 일컫는 말 (이웃 관계)
정점의 차수(degree) -> 정점에 연결되어 있는 간선의 개수 / 인접하는 정점의 수

경로(Path)

경로 길이 -> 경로를 구성하는 간선의 수

싸이클(Cycle)

두 정점간의 경로에서 동일한 정점을 두 번 이상 거치는 경로

연결성(Connectivity)

무방향성 그래프 내에서 두 정점 사이에 경로가 존재

그래프는 정점의 모음과 이 정점을 잇는 간선의 모음간의 결합

정점의 집합을 V, 간섭의 집합을 E, 그래프를 G 라고 했을 때
G = (V, E) 이다.

간선의 종류에 따라

무방향 그래프(undirected graph) : 양방향 (A, B) = (B, A)
방향 그래프(directed graph) : 방향성이 존재 <A, B> ≠ <B, A>
가중치 그래프(weighted graph), 네트워크(network) : 비용이나 가중치

그래프의 표현 방식에 따라 알고리즘의 시간 복잡도가 바뀔 수 있기 때문에 신중하게 선택

간선이 적은 희소 그래프(sparse graph): 인접 리스트
간선이 많은 밀집 그래프(dense graph): 인접 행렬

인접 리스트로 그래프를 표현

그래프 내의 각 정점의 인접 관계를 표현하는 리스트
리스트 보다는 vector 와 같이 길이를 변경할 수 있는 배열로 구현

인접 행렬로 그래프를 표현

정점의 개수가 N개이면 N*N 행렬을 이용
i 번째 정점과 j 번째 정점의 관계를 G[i][j]에 저장
문제에서 주어지는 번호대로 저장

배열이라고 0 부터 하지 말자

그래프에서 간선의 개수가 따로 주어지지 않을 경우 최대 개수는 V^2
그래프 공간 복잡도

인접행렬

간선 정보를 행렬에 저장
2 차원 배열 이용
O(N^2)

인접리스트

정점과 연결된 간선들을 리스트로 연결
링크드 리스트 이용
O(E)

간선 리스트

간선을 배열에 순서대로 나열
1차원 배열, 정렬, 구간합 이용
O(V+E)

DFS (Depth First Search)

길이 있는 한 계속 따라 감
막다른 길이면 돌아서 나오기
DFS의 구현은 보통 재귀함수로 한다

구현이 BFS 보다 쉽다
크지 않은 조건의 경우의 수를 고려할 때 적합

BFS (Breadth First Search)

시작점에서 가까운 곳부터 차례대로 방문한다
방문 할 순서

큐로 구현

그래프 순회

그래프 탐색은 그래프의 가장 기본적인 연산
하나의 정점으로부터 시작하여 차례대로 모든 정점을 한번씩 방문
많은 문제들이 단순히 그래프의 정점을 탐색하는 것으로 해결

특정한 정점에서 다른 정점으로 갈 수 있는지 없는지
전자 회로에서 특정 단자와 단자가 서로 연결되어 있는지

DFS / BFS 이용

스패닝트리(Spanning Tree)

그래프 내의 모든 정점을 포함하는 트리
싸이클을 포함해서는 안 된다
통신 네트워크 구축: 최소의 링크를 사용하여 네트워크를 구축하고 싶은 경우

최소비용 스패닝트리(MST: Minimum Spanning Tree)

네트워크에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결하는 트리
간선에 가중치 속성을 부여, 각 간선이 갖고 있는 가중치의 합이 최소가 되는 트리
응용

도로 건설 - 도시들을 모두 연결하면서 도로의 길이가 최소가 되도록 하는 문제
전기 회로 - 단자들을 모두 연결하면서 전선의 길이가 최소가 되도록 하는 문제
통신 - 전화선의 길이가 최소가 되도록 전화 케이블 망을 구성하는 문제
배관 - 파이프를 모두 연결하면서 파이프의 총 길이가 최소가 되도록 연결하는 문제

MST 알고리즘

Kruskal 알고리즘

그래프 내의 모든 간선을 가중치의 오름차순으로 정렬
싸이클이 형성되지 않으면서 간선을 최소 스패닝 트리에 추가
싸이클 검사에는 union-find 알고리즘이 사용

집합들의 합집합을 구하고 집합의 원소가 어떤 집합에 속하는지를 계산하는 알고리즘

Prim 알고리즘

그래프와 노드가 하나도 없는 최소 스패닝 트리에서 시작
그래프의 임의의 정점을 시작 정점으로 선택하여 최소 스패닝 트리의 루트 노드로 삽입
MST 에 삽입되어 있는 정점들과 이 정점들의 모든 인접 정점 사이에 있는 간선의 가중치를 조사하여 가장 작은 것을 MST 에 삽입한다. 단, 싸이클을 형성해서는 안 된다.
이 과정을 반복하다가 모든 정점이 연결되면 종료

최단 경로(Shortest path)

최단 경로 문제

네트워크에서 정점 i와 정점 j를 연결하는 경로 중에서 간선들의 가중치 합이 최소가 되는 경로를 찾는 문제
간선의 가중치는 비용, 거리, 시간 등

최단 거리

한 정점에서 다른 정점으로 가는 최단 거리를 구하는 문제
간선의 가중차기 모두 1 인 경우

BFS 를 이용해서 구할 수 있다
소스에서 step 이 바로 시작정점에서 거리

간선의 가중치가 다른 경우

시작정점에서 특정 목표 정점까지 최단거리 (단일 시작점)

다익스트라(Dijkstra) 알고리즘

시작 정점 V로부터의 최단 경로가 이미 발견된 정점들의 집합 S
distance 배열: 최단 경로를 알려진 정점만을 통하여 각 정점까지 가는 최단 경로의 길이
매 단계에서 가장 distance 값이 적은 정점을 S에 추가한다

벨만포드 알고리즘: 간선에 음수가 있을 경우

모든 쌍에 대해 최단거리

플로이드(Floyd) 알고리즘
모든 정점사이의 최단 경로를 한 번에 찾아주는 알고리즘

정점 k를 거쳐서 가지 않는 경우

정점 i 에서 j 로 가는 최단 거리는 weight[i][j]

정점 k를 거쳐서 가는 경우

weight[i][k] + weight[k][j]

최단 거리는 둘 중의 작은 값

시간복잡도: O(V^3)

네트워크 유량

최대 유량 문제

각 간선에 대해 길이 뿐만이 아니라 용량을 정의했을 때 풀 수 있는 문제

각 간선이 용량을 갖는 그래프에서 두 정점 사이에 얼마나 많은 '흐름' 혹은 유량(flow)을 보낼 수 있는지를 계산하는 문제를 네트워크 유량 문제
그래프와 별 상관이 없어 보이는 다양한 최적화 문제들을 푸는 데도 이용
유량 네트워크(flow network)란 각 간선에 용량(capacity)이라는 추가 속성이 존재하는 방향 그래프

정점 u 에서 v 로 가는 간선의 용량 c(u, v), 실제 흐르는 유량 f(u, v)
용량 제한 속성 : f(u, v) ≤ c(u, v)
유량의 대칭성 : f(u, v) == -f(v, u) 음수의 유량
유량의 보존 : 각 정점에 들어오는 유량과 나가는 유량의 양은 같음
소스(source): 유량이 시작되는 정점
싱크(sink): 유량이 도착하는 정점
정리: 네트워크 유량 문제는 이렇게 소스와 싱크 사이에 흐를 수 있는 최대 유량을 계산하는 문제

포드-풀커슨(Ford-Fulkerson) 알고리즘

위상 정렬(Topological sort)

방향성 그래프에서 간선 <u, v>가 있다면 정점 u는 정점v 를 선행한다고 말하며, 각 정점들의 선행 순서를 위배하지 않으면서 모든 정점을 나열하는 것을 말한다
모든 방향 간선이 왼쪽에서 오른쪽으로 향할 수 있도록 수평선을 따르는 정점의 나열

깊이 우선 탐색을 이용한 위상 정렬

리스트를 하나 준비한다
그래프에서 진입 간선이 없는 정점에 대해 깊이 우선 탐색을 수행하고, 탐색 중에 더 이상 옮겨갈 수 있는 인접 정점이 없는 정점을 만나면 이 정점을 리스트의 새로운 헤드로 입력한다
더 이상 방문할 정점이 없을 때까지 반복하고 깊이 우선 탐색을 종료하면, 리스트에는 위상 정렬된 리스트가 남는다

트리

계층 관계를 갖는 객체들을 표현하기 위해 만들어진 자료 구조
실제 계층 관계가 없는 자료들을 트리로 표현해서 같은 연산을 더 빠른게 할 수 있는 경우가 많아서 다른 용도로 더 많이 사용된다 (탐색형 자료구조)
뿌리(Root), 가지(Branch), 잎(Leaf)으로 이루어진 자료구조
부모-자식 관계의 노드들로 구성(부모, 자식, 형제(sibling))
경로

"A, B, C" 는 A 에서 C 까지의 경로

깊이(Depth)

루트 노드에서 해당 노드까지의 경로의 길이
레벨(Level) - 같은 깊이를 가지는 노드의 집합
높이(Height) - "가장 깊은 곳"에 있는 잎 노드까지의 깊이

차수(Degree)

자식 노드의 개수
트리의 차수는 트리 내에 있는 노드 중에 중에서 자식 노드가 가장 많은 노드의 차수를 말함

노드(Node)

트리의 구성 요소
단말 노드: 자식이 없는 노드
비단말 노드: 적어도 하나의 자식을 가지는 노드

루트(Root): 부모가 없는 노드
서브 트리: 하나의 노드와 그 자손 노드들로 이루어진 트리
트리의 표현

배열표현법

모든 이진트리를 포화이진트리라고 가정하고, 각 노드에 번호를 붙여서 그 번호를 배열의 인덱스로 삼아 노드의 데이터를 배열에 저장하는 방법
왼쪽에서 오른쪽으로 순차적으로 각 노드 번호를 부여한다. 루트의 번호를 1 로 하고, 레벨 n 에 있는 노드에 대해서 왼쪽부터 오른쪽으로 2ⁿ 부터 2ⁿ⁺¹ - 1 까지 번호를 부여한다

루트 1 은 레벨 0
다음 2 3 은 레벨 1
다음 4 5 6 7 은 레벨 2

다음과 같은 규칙이 생성이 된다

노드 번호가 i 인 노드의 부모 노드 번호 => i/2
노드 번호가 i 인 노드의 왼쪽 자손 노드 번호 => i*2
노드 번호가 i 인 노드의 오른쪽쪽 자손 노드 번호 => i*2 + 1
레벨 n 의 노드들의 시작 번호 => 2ⁿ
레벨 n 의 최대 노드 수 => 2ⁿ
높이가 h 인 이진 트리를 위한 배열의 크기 => 2^h+1 - 1

링크표현법

포인터를 이용하여 부모 노드가 자식 노드를 가리키게 하는 방법

이진 트리(Binary Tree)

모든 노드가 2 개의 서브 트리를 가지고 있는 트리
서브 트리는 공집합일 수 있다
서브 트리간의 순서가 존재

이진 트리의 성질

노드의 개수가 n 이면, 간선의 개수는 n-1
높이가 h인 이진트리의 경우, 최소 h개의 노드를 가지며 최대 2^h-1개의 노드를 가진다
n개의 노드를 가지는 이진트리의 높이는 최대 n이거나 최소 log₂(n+1)

포화 이진 트리(Full Binary Tree)

모든 노드가 대대손손이 자식을 둘 씩 가지고 있는 이진 트리

완전 이진 트리(Complete Binary Tree)

잎 노드들이 트리의 왼쪽부터 차곡차곡 채워진 트리

높이 구현 트리(Height Balanced Tree)

루트 노드를 기준으로 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 1 이상 차이 나지 않는 이진 트리

완전 높이 균형 트리(Completely Height Balanced Tree)

루트 노드를 기준으로 왼쪽 하위 트리와 하위 트리의 높이가 같은 이진 트리

순회(Traversal)

트리의 노드들을 체계적으로 방문하는 것
전위 순회(Preorder traversal) : VLR

루트 => 왼쪽 자손 => 오른쪽 자손
깊이 우선 순회(Depth First Traversal)

중위 순회(Inorder traversal) : LVR

왼쪽 자손 => 루트 => 오른쪽 자손
대칭 순회(Symmetric Traversal)

후위 순회(Postorder traversal) : LRV

왼쪽 자손 => 오른쪽 자손 => 루트

레벨 순서 순회(Level Order)

모든 노드를 낮은 레벨부터 차례대로 순환
너비 우선 순회(Breadth First Traversal)

예)

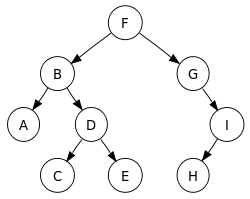
전위 순회: F, B, A, D, C, E, G, I, H (root, left, right)
중위 순회: A, B, C, D, E, F, G, H, I (left, root, right)
후위 순회: A, C, E, D, B, H, I, G, F (left, right, root)
레벨 순서 순회: F, B, G, A, D, I, C, E, H

수식 트리

수식 이진 트리(Expression Binary Tree)
수식을 표현하는 이진 트리

연산자는 루트 노드이거나 가지 노드

비단말노드: 연산자(Operator)
단말노드: 피연산자(Operand)

피연산자는 모두 잎 노드

가장 아래에 있는 하위 수식 트리(잎노드)로부터 수 또는 계산 결과를 병합해 올라가는 과정을 반복하여 계산을 수행
후위 순회를 사용
수식 트리의 구축

중위 표기식보다는 후위 표기식을 이용해 트리를 구축하는 것이 수월

이진 탐색 트리

탐색 작업을 효율적으로 처리가 위한 자료구조로 모든 원소는 서로 다른 유일한 키를 가지고 있다. 탐색(Searching), 삽입(Insertion), 삭제(Deletion) 시간은 트리의 높이만큼 시간이 걸리며, 시간복잡도는 O(h) 이다.

힙(Heap)은 "완전 이진트리"에 있는 노드 중에서 키값이 가장 큰 노드나 키값이 가장 작은 노드를 찾기 위해서 만든 자료구조이다. 최대 힙과 최소 힙이 있고, 힙의 키를 우선순위로 활용하여 우선순위 큐를 구현할 수 있다

최대 힙(Max Heap)

키값이 가장 큰 노드를 찾기 위한 완전 이진트리
부모노드의 키값 > 자손노드의 키값
루트노드는 키값이 가장 큰 노드

최소 힙(Min Heap) 은 최대 힙의 반대
힙의 삽입과 삭제 연산이 있다
가장 큰(작은) 원소를 찾는 데 최적화된 형태의 이진 트리
우선순위 큐를 쉽게 구현
부모 노드가 가진 원소는 항상 자식 노드가 가진 원소 이상
가장 큰(작은) 원소는 항상 트리의 루트
모양 규칙

마지막 레벨을 제외한 모든 레벨에 노드가 꽉 차 있어야 한다
마지막 레벨에 노드가 있을 때는 항상 가장 왼쪽부터 순서대로 채워져야 한다

배열을 이용하여 구현 가능

0 이 루트
A[i] 노드의 왼쪽 자손: A[2*i + 1]
A[i] 노드의 오른쪽 자손: A[2*i + 2]
A[i] 노드의 부모: A[(i-1)/2]
삽입

맨 끝에 추가후 부모와 계속 비교

삭제

루트 삭제 후 맨 마지막 원소를 루트에 덮어 씌우고, 대소 관계 조건을 만족시킨다(자식과 비교)
최소는 가능한 자식 중에 더 작은 값과 교환
최대는 가능한 자식 중에 더 큰 값과 교환

구간 트리(Segment Tree)

저장된 자료들을 적절히 전처리해 그들에 대한 질의들을 빠르게 대답 가능

일차원 배열의 특정 구간에 대한 질문을 빠르게 대답하는데 사용

기본: 주어진 배열의 구간들을 표현하는 이진 트리를 만드는 것(전처리)

루트: 항상 배열의 전체 구간 [0, n-1]
왼쪽 자식과 오른쪽 자식은 각각 해당 구간의 왼쪽 반과 오른쪽 반을 표현

대표 예: 특정 구간의 최소치를 찾는 문제

구간 최소 쿼리(RMQ, Range Minimum Query)
루트 노드: 배열의 1 번 원소
노드 i 의 왼쪽 자손: 2 * i
노드 i 의 오른쪽 자손: 2 * i + 1 번
배열의 길이: 가장 가까운 2의 거듭제곱으로 n을 올림 후 2 를 곱한 값 혹은 4n

LCA(Lowest Common Ancestor)문제

트리에서 두 노드의 공통조상 중 가장 가까운 조상 노드를 구하는 문제

한 노드가 다른 하나의 조상인 경우 최소 공통 조상은 둘 중 위 노드가 된다는 데 유의

BIT: Binary Index Tree 는 일반적으로 누적합만 활용할 수 있다
IDT: Index Tree 는 Complete Binary Tree 로 구성된 Segment Tree 를 말한다

정해진 구간의 합, 최댓값, 최솟값 등을 lg n 의 시간에 구할 수 있으며, 갱신 또한 lg n 시간에 처리할 수 있는 매우 효율적인 자료구조
기본적인 구조는 원본 데이터를 complete binary tree 의 단말노드에 배치하고, 그 값의 부모노드를 특정한 의미를 가지는 index로 활동하는 방법이다
가장 효율적인 표현 방법은 일차원 배열을 이용하고, 원본 데이터가 n개인 경우에 n이상인 가장 작은 2^k값을 기준으로 설정하고, 이 값의 2 배에서 1 을 뺀 개수의 원소를 가지는 배열로 구성
최대 LIS (Longest Increasing Subsequence) 를 O(lg n) 만에 빠르게 찾아낼 수 있다

트립(treap) - A Randomized Binary Search Tree (Tree + Heap)

구현이 간단한 이진 검색 트리
트리의 형태가 추가 순서가 아닌 난수에 의해 임의대로 결정
추가나 삭제되더라도 트리 높이의 기대치는 항상 일정
트립의 루트는 N 개의 노드 중 최대의 우선순위를 갖는 노드
트립의 조건

이진 검색 트리의 조건: 모든 노드에서 왼쪽 서브트리의 원소는 작고, 오른쪽 서브트리의 원소는 크다
힙(heap)의 조건: 모든 노드의 우선순위는 각자의 자식 노드보다 크거나 같다

유니온-파인드(Union-Find) 자료 구조

상호 배타적 집합(disjoint set)을 표현

공통 원소가 없는, 상호 배타적인 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료 구조

초기화
합치기(Union/Merge) 연산
찾기(Find) 연산

알고리즘 문제 해결 전략: 코드 25.2

그리디(Greedy)

알고리즘 설계에 있어서 중요한 기법중의 하나
결정을 해야 할 때마다 그 순간에 가장 좋다고 생각되는 것을 해답으로 선택함으로써 최종적인 해답에 도달
항상 최적의 답을 해주는지를 반드시 검증해야 한다
최적의 해답을 주는 것으로 증명된 알고리즘

Kruskal 알고리즘

완전 탐색과 동적 계획법 알고리즘

같은 점

여러 개의 조각으로 쪼개고, 각 단계마다 답의 한 부분을 만들어 간다는 점

다른 점

모든 선택지를 고려해 보고 그중 전체 답이 가장 좋은 것을 찾음
각 단계마다 지금 당장 가장 좋은 방법만을 선택

지금의 선택이 앞으로 남은 선택에 어떤 영향을 끼칠지는 고려하지 않는다

두 가지 경우로 제한

탐욕법을 사용해도 항상 최적해를 구할 수 있는 문제를 만난 경우
시간이나 공간적 제약으로 다른 방법으로 최적해를 찾기 너무 어려운 경우

최적은 아니지만 임의의 답보다는 좋은 답을 구하는 용도

유용하게 사용되는 문제 중 유명한 예

활동 선택 문제(activity selection problem)

회의실 예약 문제의 경우에 가장 먼저 끝나는 회의부터 선택하는 것

정당성의 증명

탐욕적 선택 속성(Greedy choice property)

동적 계획법처럼 답의 모든 부분을 고려하지 않고 탐욕적으로만 선택하더라도 최적해를 구할 수 있다는 것

최적 부분 구조(Optimal substructure)

부분 문제의 최적해에서 전체 문제의 최적해를 만들 수 있음을 보인다

메타휴리스틱(Metaheuristic) 알고리즘

최적화 알고리즘의 한 종류
좋은 답을 빠르게 찾아낼 수 없는 문제의 근사해를 구하기 우해 주로 사용
국소 탐색(Local search)이나 시뮬레이티드 어닐링(Simulated annealing)이 구현과 튜닝이 가장 간단해 자주 사용

KMP 알고리즘 (참고: http://bowbowbow.tistory.com/6)

커누스-모리스-프랫Knuth-Morris-Pratt) 알고리즘
문자열 검색 문제
텍스트의 길이 N, 검색 문자를 M 이라고 할 때, O(M+N) 으로 처리가능
불일치가 일어났을 때 지금까지 일치한 글자의 수를 이용해 다음으로 시도해야 할 시작 위치를 빠르게 찾아냄
전처리 과정에서 배열 pi[] 를 계산

pi[i] = N[...i]의 접두사도 되고 접미사도 되는 문자열의 최대 길이
부분 일치 테이블(partial number table)

자료구조

자료구조

프로그램이 자료를 저장하는 방식
두 가지 목적을 위해서 고안된 것들

추상화

자료를 좀 더 알아보기 쉽고, 이해하기 쉬운 형태로 저장하기 위한 고민의 결과물

최적화

프로그램의 동작 속도를 빠르게 하기 위한 것
탐색 자료 구조의 경우 표현방식과 더불어 다루는 방법(알고리즘)도 같이 정의

선형 자료구조

왼쪽에서 오른쪽 혹은 위에서 아래로 나열된 형태를 하고 있는 것
정적 배열 (C++ 자료형[])
동적 배열 (C++ STL vector)

더 나은 성능을 위해서 reserve() 와 resize() 를 사용

정렬과 검색

O(n²) 정렬 알고리즘: 버블(Bubble), 선택(Selection), 삽입(Insertion) 등
O(nlogn) 정렬 알고리즘: 병합(Merge), 힙(Heap), 퀵(Quick) 등

STL algorithm: sort, partial_sort, stable_sort

특수 목적 정렬 알고리즘: O(n) 계수(Counting), 기수(Radix), 버킷(Bucket) 등
O(n) 선형 탐색
O(logn) 이진 탐색: C++ STL algorithm 내의 lower_bound, upper_bound, binary_search
O(1) 해싱

불린(Boolean) 배열: C++ STL bitset
불린 값들로 이루어진 작은 집합을 가볍게 다루기 위한 비트마스크

비선형 자료구조 (내장 라이브러리)

균형 잡힌 이진 검색 트리

C++ STL map

페어로 된(예, 키 -> 값) 자료의 모음을 동적으로 처리
삽입, 검색, 삭제 작업을 O(logn)

C++ STL set

키만을 저장
보통, 특정한 키가 존재하는지 여부를 효율적으로 판별하려 할 때만 유용

힙(Heap)

완전 트리
힙은 우선순위 큐를 모델링할 때 유용한 자료구조
O(logn) 으로 가장 높은 우선순위를 갖는 원소(최대 혹은 최소)를 큐에서 꺼내는 작업과 새로운 원소 v를 큐에 추가하는 작업을 지원
MST 를 구하기 위한 프림(및 크루스칼) 알고리즘
단일 시작점 최단 경로 문제를 위한 다익스트라 알고리즘
A* 탐색 알고리즘
C++ STL priority_queue

해시 테이블

C++11 STL unordered_map
잘 안쓰임

추상형 자료구조

스택
큐

BFS (Breadth First Search) 너비 우선 탐색

탐색형 자료구조

트리

이진 탐색 트리
힙
구간 트리

해시

분류

동적 배열
연결 리스트
문자열 탐색

KMP 알고리즘

문자열 처리

접미사 배열(suffix array)

트리
그래프
비트마스크(bitmask)

엄밀하게 자료구조는 아니지만, 많이 쓰인다
정수의 이진수 표현을 자료 구조로 쓰는 기법
비트 연산자

a & b: 비트별로 AND 연산
a | b: 비트별로 OR 연산
a ^ b: 비트별로 XOR 연산
~a: 비트별 NOT 연산 결과
a << b: 왼쪽으로 b 비트 시프트
a >> b: 오른쪽으로 b 비트 시프트

집합의 구현

가장 중요한 사용 사례(예, 20 개를 이용)
공집합

int a = 0;

꽉 찬 집합

int a = (1<<20) - 1; // 1 을 20 bit 이동하고 1 을 뺀다

원소 추가 p (0 <= p < 20)

a |= (1 << p);

원소의 포함 여부

if (a & (1 << p)) ~~

원소의 삭제

a &= ~(1 <<p);

원소의 토글

a ^= (1 << p);

두 집합의 연산

집합간의 연산을 빠르게 할 수 있다는 것이 큰 장점
합집합

added = (a | b);

교집합

intersection = (a & b);

차집합

removed = (a & ~b);

하나에만 포함된 원소들의 집합

toggled = (a ^ b);

집합의 크기

재귀호출
내장명령어

최소 원소 찾기

int first = (a & -a);

최소 원소 지우기

a &= (a - 1);

모든 부분 집합 순회하기

for (int subset = a; subset; subset = ((subset-1) & a)) {}

2016년 4월 24일 일요일

알고리즘 문제 풀이에서의 qsort 사용 주의점

http://www.cplusplus.com/reference/cstdlib/qsort/

에 있는 sample code 에서는 아래와 같은 예제코드가 있는데,

이 코드를 그대로 사용하면 알고리즘 문제 풀이시에는 문제가 될 수 있습니다.

qsort 의 마지막 인자로 필요한 compare 함수 예제 코드

 int compare (const void * a, const void * b)  
 {  
   return ( *(int*)a - *(int*)b );  
 }

https://www.acmicpc.net/problem/1920 수 찾기

문제의 경우에는 입력값을 sort 해야 하는데, qsort 함수에 필요한 compare 함수 구현시에 예제코드를 그대로 사용하면 overflow 로 문제가 틀리게 됩니다.
문제 본문에 int 범위 전체를 사용하는 입력값을 언급했는데, 별 생각없이 넘어간 게 문제였고, 이런 주의사항은 절대 지나쳐서는 안 되는 사항임을 자주 잊게 되네요. -_-

compare 함수 parameter 설명에 있는 그대로 구현해야 문제가 없게 됩니다.

 int compare(const void* a, const void* b) {  
   if (*(int *)a < *(int *)b) {  
     return -1;  
   }  
   else if (*(int *)a == *(int *)b) {  
     return 0;  
   }  
   else {  
     return 1;  
   }  
 }

2016년 4월 21일 목요일

피보나치 문제 풀이

피보나치 문제 풀이는 baekjoon 님의 블로그를 참고하자. : )

피보나치 수를 구하는 여러가지 방법

https://www.acmicpc.net/blog/view/28

(회고) acmicpc 문제 1004 번: 어린 왕자, 원 안에 점이 있는지

https://www.acmicpc.net/problem/1004 어린 왕자

문제 요점은 각각의 원 안에 시작점과 끝점이 있는지 여부

한 점과 원의 중심점의 길이와 반지름의 길이를 비교해서
원 안에 있는지 원에 걸쳐 있는지 밖에 있는지 알 수 있다

어린 왕자 문제는 원과 겹치는 부분이 없으니 시작점과 끝점의
상태가 다른 상태(안쪽/바깥쪽)인지 확인해서 숫자 늘려준다....

in 인지 확인

 bool in(int x, int y, int cx, int cy, int r) {  
   if ( (x - cx)*(x - cx) + (y - cy)*(y - cy) > r*r )  
     return false;  
   else  
     return true;  
 }

다른 상태인지 확인

     while (N--) {  
       scanf("%d %d %d", &cx, &cy, &r);  
       if (in(X1, Y1, cx, cy, r) != in(X2, Y2, cx, cy, r))  
         count++;  
     }  
     printf("%d\n", count);

* 유사 문제
https://www.acmicpc.net/problem/1002 터렛

2016년 4월 20일 수요일

(회고) acmicpc 문제 1010 번: 다리 놓기

https://www.acmicpc.net/problem/1010 다리 놓기

문제가 n 개 중에 m 개 고르는 문제인데,
수학적 지식이 이제 없는 상태라 처음에는 단순히 전체 탐색을 시도

 #include <cstdio>  
 int A, B;  
 int num;  
 void find(int index, bool select, int count) {  
     if (index >= B)  
         return;  
     if (A == count) {  
         num++;  
         return;  
     }  
     if (B - index < A - count) {  
         return;  
     }  
     find(index + 1, true, count + 1);  
     find(index + 1, false, count);  
 }  
 int main(void) {  
     int N;  
     scanf("%d", &N);  
     while (N--) {  
         scanf("%d %d", &A, &B);  
         find(0, true, 1);  
         find(0, false, 0);  
         printf("%d\n", num);  
         num = 0;  
     }  
     return 0;  
 }

시간 초과 발생

위 코드 이용해서 아래 테이블을 만들어서 규칙을 확인
=> 특정 i, j 값부터 이전 두 값(i, j-1 와 i-1, j-1)의 합

init() 함수에서 미리 값을 계산해 두고 입력시 바로 결과 출력하는 방식으로 변경해서 처리

 #define MAX 30  
 int table[MAX + 1][MAX + 1];  
 void init() {  
   for (int i = 1; i <= MAX; i++) {  
     for (int j = i; j <= MAX; j++) {  
       if (i == 1 || i == j - 1)  
         table[i][j] = j;  
       else if (i == j)  
         table[i][j] = 1;  
       else  
         table[i][j] = table[i][j - 1] + table[i - 1][j - 1];  
     }  
   }  
 }

문제 풀고 short code 를 보면 머리가 나쁘면 손발이 고생이라는 게 느껴짐... -_-

2016년 4월 18일 월요일

알고리즘 문제 풀이: 자주 쓰이는 코드3

* 초보자를 위한 추천 읽을꺼리 강의자료에서 모음

1) SWAP

 // 템플릿을 사용하여 범용성 있게  
 template<typename T>    
 // 레퍼런스를 사용하여 빠르게  
 void swap(T& a, T& b) {    
   T t = a;  
   a = b;  
   b = t;  
 }

2) MAX

 int MAX(int p, int q) {  
   return p > q ? p : q;  
 }

3) MIN

 int MIN(int p, int q) {  
   return p > q ? q : p;  
 }

4) ABS

 int abs(int a) {  
   return a > 0 ? a : ‐a;  
 }

5) Log 출력

 #if 1  
 #define PA(X, ...) printf(X, __VA_ARGS__)  
 #define P(X) printf(X)  
 #else  
 #define PA(X, ...)  
 #define P(X)  
 #endif  
 int main() {  
   P("Hello!");  
   PA(" %s", "world");  
 }

6) 수행시간 측정

 #include <ctime> or <time.h>  
 clock_t = t1, t2;  
 t1 = clock();  
 {  
   Code  
 }  
 t2 = clock();  
 printf("time: %lf\n", (double)(t2-t1)/CLOCKS_PER_SEC);

7) 나머지 연산

 (a + b) % m = ( a % m + b % m) % m  
 (a * b) % m = ( a % m * b % m) % m

8) BigInteger for C++
C에서 BigInteger 사용에 관한 백준님의 추천링크
https://www.acmicpc.net/board/view/3125
=> http://stackoverflow.com/questions/4507121/c-big-integer
=> http://codeforces.com/blog/entry/16380

9) quick sort

 void quickSort(int arr[], int left, int right) {  
     int i = left, j = right;  
     int tmp;  
     int pivot = arr[(left + right) / 2];  
     while (i <= j) {  
         while (arr[i] < pivot)  
             i++;  
         while (arr[j] > pivot)  
             j--;  
         if (i <= j) {  
             tmp = arr[i];  
             arr[i] = arr[j];  
             arr[j] = tmp;  
             i++;  
             j--;  
         }  
     };  
     if (left < j)  
         quickSort(arr, left, j);  
     if (i < right)  
         quickSort(arr, i, right);  
 }

10) merge sort

 void merge(int arr[], int copy[], int start, int end) {  
   int mid = (start + end) / 2;  
   int i = start;  
   int j = mid + 1;  
   int k = start;  
   while (i <= mid && j <= end) {  
     if (arr[i] <= arr[j])  
       copy[k++] = arr[i++];  
     else  
       copy[k++] = arr[j++];  
   }  
   while (i <= mid)  
     copy[k++] = arr[i++];  
   while (j <= end)  
     copy[k++] = arr[j++];  
   for (int i = start; i <= end; i++)  
     arr[i] = copy[i];  
 }  
 void sort(int arr[], int copy[], int start, int end) {  
   if (start == end)  
     return;  
   int mid = (start + end) / 2;  
   sort(arr, copy, start, mid);  
   sort(arr, copy, mid + 1, end);  
   merge(arr, copy, start, end);  
 }

알고리즘 문제 풀이: 자주 쓰이는 코드2

* 초보자를 위한 추천 읽을꺼리 강의 자료에서 모음

1) 이분 탐색

 while (lower_bound <= upper_bound) {  
   int mid = (lower_bound + upper_bound) / 2;  
   if (test(mid) == true) {  
     answer = mid;  
     upper_bound = mid - 1;  
   } else {  
     lower_bound = mid + 1;  
   }  
 }

2) 행렬을 이용한 그래프 표현

 int V; // 정점의 수  
 int E; // 간선의 수  
 int G[MAX_V + 1][MAX_V + 1]; // 인접행렬  
 scanf("%d", &V);  
 scanf("%d", &E);  
 for (int i = 0; i < E; ++i) {  
   int u, v;  
   scanf("%d%d", &u, &v);  
   G[u][v] = 1; // 정점 u와 v는 연결  
   G[v][u] = 1; // 정점 v와 u는 연결  
 }

3) 행렬을 이용한 그래프 표현(가중치)

 int V; // 정점의 수  
 int E; // 간선의 수  
 int G[MAX_V + 1][MAX_V + 1]; // 인접행렬  
 scanf("%d", &V);  
 scanf("%d", &E);  
 // 인접행렬 초기화  
 for (int i = 0; i < V; ++i) {  
   for (int j = 0; j < V; ++j) {  
     G[i][j] = -1;  
   }  
   G[i][i] = 0;  
 }  
 // 간선을 입력 받아 인접행렬을 채운다  
 for (int i = 0; i < E; ++i) {  
   int u, v, w;  
   scanf("%d%d%d", &u, &v, &w);  
   G[u][v] = w;  
   G[v][u] = w;  
 }

4) DFS - 인접행렬

 bool visited[MAX_N + 1];  
 bool finished[MAX_N + 1];  
 void DFS(int u) {  
   // 이미 방문했는지 검사  
   if (visited[u]) {  
     return;  
   }  
   // u번째 정점을 지금 방문함  
   visited[u] = true;  
   printf("%d\n", u);  
   // 인접한 정점을 방문  
   for (int v = 1; v <= N; ++v) {  
     if (v == u) continue;  
     if (A[u][v]) {  
       DFS(v);  
     }  
   }  
   // u번째 정점 방문을 마침  
   finished[u] = true;  
 }

5) DFS

 int Y, X;  
 map[MAX_ROW + 1][MAX_COL + 1];  
 visited[MAX_ROW + 1][MAX_COL + 1];  
 void dfs(int y, int x) {  
   // 지도의 경계를 벗어나는지 검사  
   if (y < 0 || y >= Y || x < 0 || x >= X) {  
     return;  
   }  
   // 이미 방문했는지 검사  
   if (visited[y][x]) {  
     return;  
   }  
   // (y, x)를 방문  
   visited[y][x] = true;  
     
   // 인접한 칸을 방문  
   dfs(y - 1, x);  
   dfs(y, x - 1);  
   dfs(y + 1, x);  
   dfs(y, x + 1);  
 }

6) BFS - 인접행렬

 push(int v) {  
   if (visited[v] == false) {  
     pushQueue(v);  
     visited[v] = true;  
   }  
 }  
 ...  
 push(start);  
 int step = 0;  
 while (!queueIsEmpty()) {  
   step++;  
   int queue_size = queueSize();  
   for (int i = 0; i < queue_size; ++i) {  
     int u = pop();  
     printf("%d\n", u);  
     for (int v = 1; v <= N; ++v) {  
       if (u != v && G[u][v]) {  
         push(v);  
       }  
     }  
   }  
 }

7) BFS - 격자

 dy[] = { 1, 0, -1, 0 };  
 dx[] = { 0, 1, 0, -1 };  
 ...  
 push(startPoint);  
 int step = 0;  
 while (!queueIsEmpty()) {  
   step++;  
   int queue_size = queueSize();  
   for (int i = 0; i < queue_size; ++i) {  
     Point p = pop();  
     printf("%d %d\n", p.x, p.y);  
     for (int d = 0; d < 4; ++d) {  
       Point next;  
       next.x = p.x + dx[d];  
       next.y = p.y + dy[d];  
       push(next);  
     }  
   }  
 }

8) BFS - 나이트

 dy[] = { 2, 1, -1, -2, -2, -1, 1, 2};  
 dx[] = { 1, 2, 2, 1, -1, -2, -2, -1};  
 ...  
 push(startPoint);  
 int step = 0;  
 while (!queueIsEmpty()) {  
   step++;  
   int queue_size = queueSize();  
   for (int i = 0; i < queue_size; ++i) {  
     Point p = pop();  
     printf("%d %d\n", p.x, p.y);  
     for (int d = 0; d < 8; ++d) {  
       Point next;  
       next.x = p.x + dx[d];  
       next.y = p.y + dy[d];  
       push(next);  
     }  
   }  
 }

9) 플로이드 알고리즘

2016년 4월 16일 토요일

입력시점에 데이터를 처리하는 여러가지 방법들

1) 입력시에 좌표를 저장하여 검색을 안 해도 되도록
2578번: 빙고 (https://www.acmicpc.net/problem/2578)

 typedef struct {  
   int y, x;  
 } POS;  
 POS num[SIZE*SIZE + 1];  
 ...  
   for (int i = 0; i < SIZE; i++)  
     for (int j = 0; j < SIZE; j++) {  
       int n;  
       scanf("%d", &n);  
       num[n].y = j;  
       num[n].x = i;  
     }  
 ...

입력시점에 i, j 값을 y, x 에 저장해 두면, 나중에 bingo 계산시에 n 으로 접근해서 y, x 값을 바로 알수 있다.

2) 입력시점에 -1, 0, 1 의 세 값을 처리하기 편한 값으로 변환
1780번: 종이의 개수 (https://www.acmicpc.net/problem/1780)

-1, 0, 1 로 처리하기 보다는 0, 1, 2 가 생각하기도 편하고, 나중에 개수 셀 때에도 index 로 바로 활용할 수 있어서 처리하기도 편하다

   for (int i = 0; i < N; i++) {  
     for (int j = 0; j < N; j++) {  
       scanf("%d", &a[i][j]);  
       a[i][j]++;  
     }  
   }

3) 입력시점에 소트하지 않아도 되도록
10989번: 수 정렬하기 3 (https://www.acmicpc.net/problem/10989)

입력 데이터가 최대 10000000 이지만, 개별 데이터의 최대값은 10000 이기 때문에 중복 데이터의 개수를 세는 방식으로 처리한다. 1~10000 까지 각 값이 몇 개씩 있는지만 세면 된다.

 #define MAX 10000  
 int number[MAX+1];  
 int main(void) {  
   int N, temp;  
   scanf("%d", &N);  
   for(int i = 0; i < N; i++) {  
     scanf("%d", &temp);  
     number[temp]++;   
   }  
   for (int i = 1; i <= MAX; i++) {  
     if (number[i] > 0) {  
       for (int j = 0; j < number[i]; j++) {  
         printf("%d\n", i);  
       }  
     }  
   }

4) 입력 데이터로 하나의 경로에 여러 개의 다른 값이 존재하는 경우
11404번: 플로이드 (https://www.acmicpc.net/problem/11404)

입력 데이터가 중복으로 제공이 되는데, 최소 비용 문제이니 중복되는 데이터 중에 가장 작은 비용으로 설정하도록 하면 된다.
시작 도시 a, 도착 도시 b, 한 번 타는데 필요한 비용 c

   for (int i = 0; i < m; i++) {  
     scanf("%d %d %d", &a, &b, &c);  
     if (weight[a][b] > c)  
       weight[a][b] = c;  
   }

2016년 4월 14일 목요일

알고리즘 문제 풀이 : 자주 쓰이는 코드1

* 초보자를 위한 추천 읽을꺼리 강의 자료에서 모음

1) 입력을 그대로 출력

   char c;  
   while ((c = getchar()) != EOF) {  
     printf("%c", c);  
   }

2) 1 부터 n 까지 합

 int sumToN(int n) {  
   return n * (n + 1) / 2  
 }

3) 간편한 최대 공약수 구하기

 int gcd(int a, int b) {  
   int great_common_divisor = 1;  
   for (int k = 1; k <= a && k <= b; ++k) {  
     if (a % k == 0 && b % k == 0) {  
       great_common_divisor = k;  
     }  
   }  
   return great_common_divisor;  
 }

 int GCD(int a, int b) {  
   while(b != 0) {  
     int r = a % b;  
     a = b;  
     b = r;  
   }  
   return a;  
 }

 int GCD(int a, int b) {  
   return b == 0 ? a : GCD(b, a % b);  
 }

4) char 변수 연산

 '0' == 48  
 'A' == 65  
 'a' == 97  
 // 정수 연산 가능  
 '0' + 1 == '1'  
 'A' + 3 == 'D'  
 'G' + 32 == 'g'  
 'p' - 32 == 'P'

4-1) char <-> int 변환

 int asciiDigitToNumber(char x) {  
   // x >= '0' && x <= '9'  
   return x - '0';  
 }  
 char numberDigitToAscii(int x) {  
   // x >= 0 && x <= 9  
   return x + '0';  
 }

4-2) 대소문자 변환

 void toCapital(char* s) {  
   for (int i = 0; s[i]; ++i) {  
     if (s[i] &gt;= 'a' &amp;&amp; s[i] &lt;= 'z') {  
       s[i] -= 32;  
     }  
   }  
 }  
 void toLower(char* s) {  
   for (int i = 0; s[i]; ++i) {  
     if (s[i] &gt;= 'A' &amp;&amp; s[i] &lt;= 'Z') {  
       s[i] += 32;  
     }  
   }  
 }

5) int 의 최대값과 큰 값으로 초기화 필요시

 int a = 2147483647; // maximum value of integer  
 int b =  987654321;

6) 문자열 세기

 int strlen(char* s) {  
   int len = 0;  
   while (s[len]) {  
     len++;  
   }  
   return len;  
 }

 int strlen(char *p) {  
   int len = 0;  
   while (*p++ != '\0') {  
     len++;  
   }  
   return len;  
 }

7) 숫자 하나씩 꺼내쓰기

 while (n > 0) {  
   int k = n % 10;  
   // do something with k  
   ...  
   n /= 10;  
 }

9) 스택

 const int MAX_STACK_SIZE = 1000;  
 int stack[MAX_STACK_SIZE + 1];  
 int stack_top;  
 void stackInit() {  
   stack_top = 0;  
 }  
 int stackSize() {  
   return stack_top;  
 }  
 bool stackIsEmpty() {  
   return stack_top == 0;  
 }  
 void stackPush(int x) {  
   stack[stack_top++] = x;  
 }  
 int stackPop() {  
   return stack[--stack_top];  
 }

10) 큐

 const int MAX_QUEUE_SIZE = 10000;  
 int queue[MAX_QUEUE_SIZE + 1];  
 int queue_head;  
 int queue_tail;  
 void queueInit() {  
   queue_head = queue_tail = 0;  
 }  
 int queueSize() {  
   return queue_tail - queue_head;  
 }  
 bool queueIsEmpty() {  
   return queueSize() == 0;  
 }  
 void queuePush(int x) {  
   queue[queue_tail++] = x;  
 }  
 int queuePop() {  
   return queue[queue_head++];  
 }

11) 반올림
반올림에 대해서 따로 처리할 필요가 없다
.2f 는 소수점 셋째 자리에서 반올림한후 소수점 둘째 자리까지 출력하라는 의미

 printf("%.2f", avg / N);

12) 덱

 #define MAX 20000  
 int queue[MAX + 1];  
 int front, rear;  
 void init(void) {  
   front = MAX / 2;  
   rear = front + 1;  
 }  
 int size(void) {  
   return rear - front - 1;  
 }  
 void push_front(int n) {  
   queue[front--] = n;  
 }  
 void push_back(int n) {  
   queue[rear++] = n;  
 }  
 bool empty(void) {  
   if (size() > 0)  
     return false;  
   else  
     return true;  
 }  
 int pop_front(void) {  
   if (size() > 0) {  
     return queue[++front];  
   }  
   else {  
     return -1;  
   }  
 }  
 int pop_back(void) {  
   if (size() > 0) {  
     return queue[--rear];  
   }  
   else {  
     return -1;  
   }  
 }  
 int qfront(void) {  
   if (size() > 0) {  
     return queue[front + 1];  
   }  
   else {  
     return -1;  
   }  
 }  
 int qback(void) {  
   if (size() > 0) {  
     return queue[rear - 1];  
   }  
   else {  
     return -1;  
   }  
 }

2016년 4월 13일 수요일

입력을 처리하는 여러 가지 방법을 정리

문자열이 입력으로 주어지고, 한 문자씩 처리해야 하는 경우

1157번: 단어 공부(https://www.acmicpc.net/problem/1157)
문제에서 시간 낭비를 한 경우를 정리한 것 입니다.

최대 1,000,000 길이를 가지는 대소문자로 이루어진 문자열이 입력으로 주어지고,
1 문자씩 처리해야 하는 상황인데, 이런 경우에 대해서는 아래와 같은 입력 처리하면 됩니다.

   char c;  
   while ((c = getchar()) != EOF && c != '\n') {  
   ....  
   }

문제 자체는 쉬운데, 입력값 처리하는데 시간을 다 보낸 경우네요.

* 추가로 적용 가능한 문제
11718번: 그대로 출력하기(https://www.acmicpc.net/problem/11718)

11719번: 그대로 출력하기 2(https://www.acmicpc.net/problem/11719)

1152번: 단어의 개수(https://www.acmicpc.net/problem/1152)

어떤 입력이 오면 중단하면 되는 경우

6588번: 골드바흐의 추측 (https://www.acmicpc.net/problem/6588) 같은 경우는
0 이 오면 중단

   while (1) {  
     scanf("%d", &N);  
     if (N == 0)  
       break;  
     // Do something  
     // Print answer  
   }  
   return 0;

5086번: 약수와 배수 (https://www.acmicpc.net/problem/5086) 같은 경우는 0 이 두 개 오면 중단

   while (1) {  
     scanf("%d %d", &A, &B);  
     if (A == 0 && B == 0)  
       break;  
     // Do something  
     // Print answer  
   }  
   return 0;

입력의 끝이 정의되어 있지 않는 경우

10951번: A + B - 4 (https://www.acmicpc.net/problem/10951) 같은 경우는
따로 끝이 정의되어 있지 않다. 이 경우는 아래와 같이 처리하면 된다.

   int A, B;  
   while (scanf("%d %d", &A, &B) != EOF)  // while (scanf("%d %d", &A, &B) == 2)
     printf("%d\n", A + B);

scanf 의 return 값은 성공적으로 입력받는 변수의 개수이기 때문에 변수 개수만큼 들어왔는지로 체크해도 된다

4999번: 아! (https://www.acmicpc.net/problem/4999) 도 비슷하게 h 가 두 번째 올때까지 처리해주면 된다.

   while (scanf("%c", &c) != EOF) {  
       if (두 번째 h 를 만나면 while 문을 중단)  
         break;  
   }

입력으로 사용되는 데이터가 중복이 있는 경우

1916번: 최소비용 구하기 (https://www.acmicpc.net/problem/1916) 같은 경우는 입력데이터를 그냥 받아서 쓰게 되면 틀리게 된다. 그래프 문제의 경우에 중복값이 전달 될 수 있는 경우를 고려해야 한다.

일반적인 경우

   for (int k = 0; k < M; k++) {  
     scanf("%d %d %d", &i, &j, &cost);  
     map[i][j] = cost;  
   }

중복데이터를 고려하는 경우(중복되는 경우 그 중 최소값이 필요)

   for (int k = 0; k < M; k++) {  
     scanf("%d %d %d", &i, &j, &cost);  
     if (map[i][j] == 0)  
       map[i][j] = cost;  
     else if (map[i][j] > cost)  
       map[i][j] = cost;  
   }

입력으로 사용되는 데이터의 순서를 고려해야 하는 경우

1991 번: 트리 순회 (https://www.acmicpc.net/problem/1991) 같은 경우는 1 차원 배열로 tree 를 구성하는 경우(예를 들어, index 1 은 root, left 는 index * 2, right 는 index*2+1)에 순차적으로 데이터가 있는 경우(예제 데이터)는 입력순으로 처리를 하면 tree 구성이 가능하다. 하지만, 제출시에 사용되는 입력값은 순차적으로 처리하면 tree 가 구성이 안 되는 것이 존재한다. 그래서, 1 차원으로 순서를 고려하면서 처리가 복잡해지기 보다는, 2 차원 배열로 자신과 자식들을 간단히 표현하고, 순차적으로 입력 받도록 한다.

 #define MAX 26  
 int tree[MAX + 1][2];  
   int N;  
   scanf("%d", &N);  
   for (int i = 0; i < N; i++) {  
     scanf("%c %c %c %c", &lf, &parent, &left, &right);  
     if (left != '.')  
       tree[parent - 'A'][0] = left - 'A';  
     if (right != '.')  
       tree[parent - 'A'][1] = right - 'A';  
   }

2016년 4월 8일 금요일

Baekjoon Online Judge 의 문제 추천 받기

* 2019.04.01 이제 운영이 되지 않는 것 같습니다.

acmicpc.net 이 주로 알고리즘 문제 풀어보는 곳인데,
다른 분들이 푸신 코드 보다가 cubelover 라는 분이 만드신 문제 추천 사이트가 있어서 소개합니다.

http://soranohana.ga/acmicpc/

접속하면 ID 를 넣는 곳이 제공이 됩니다.

이 사이트를 만드신 cubelover 님은 Level 이 96 이시네요. (2016. 4. 8 일자)

저는 해보니 Level 이 21 이네요. (2016. 4. 8 일자)

Baekjoon Online Judge 에서는 아래 메뉴로 비슷하게 제공되는 것 같습니다.

문제 - 내가 못 푼 문제

2016년 4월 7일 목요일

freopen() 사용으로 입력 출력 간편하게 처리하기

* Updated: 아래 내용은 Visual Studio 아닌 경우 (괜찮은 IDE 가 없는 Android 라든지..) 에 임시 방편으로 할 만한 내용이고, Visual Studio 같이 좋은 IDE 환경에서는 debug setting 을 이용하는 방식을 쓰면 됩니다
참고 1) http://gooddaytocode.blogspot.kr/2016/06/visual-studio.html
참고 2) http://gooddaytocode.blogspot.kr/2017/03/google-code-jam-visual-studio.html

Online Judge 사이트 문제를 보면 표준입출력으로
입력을 처리하고, 결과를 출력하면 성공이나 실패 여부를 알려주게 됩니다.

간단히 해결 가능한 문제라면 Online editor 에서 바로 작성해서 제출해도 되겠지만
어느 정도 난이도가 있는 경우에는 PC 개발환경에서 시험을 해보고 만족할 만한 상태가 되면 제출을 하게 됩니다.

PC 에서 Test 할 때에 입력이 단순 하다면
(예를 들어, N 을 입력 받아 N 을 출력하라.)

1:  #include <stdio.h>  
2:    
3:  int main(void) {  
4:    int N;  
5:    scanf("%d", &N);  
6:    printf("%d", N);  
7:    return 0;  
8:  }

Console 에 매번 입력할 만한 하지만, 복잡한 케이스라면 데이터를 매번 입력하는 것은 가급적 하지 않는 것이 정신건강에 좋을 듯 하네요.

freopen() 이라는 함수가 이런 수작업을 없앨 수 있는 방법 중에 하나인데, 아래와 같이 사용하게 되면 Console 창에 결과가 바로 출력이 됩니다.

주의: 파일 경로가 없기 때문에 Source code 파일과 동일한 경로에 존재해야 합니다.

1:  #include <stdio.h>  
2:    
3:  int main(void) {  
4:    int N;  
5:    
6:    freopen("input.txt", "r", stdin);  
7:    
8:    scanf("%d", &N);  
9:    printf("%d", N);  
10:    return 0;  
11:  }

간단하게 input.txt 에 있는 내용을 read 해서 stdin 으로 전달해 주는 것이라고 생각하면 됩니다. 역으로, console 확인하는게 귀찮으면 아래와 같이 해주면 됩니다.

1:  #include <stdio.h>  
2:    
3:  int main(void) {  
4:    int N;  
5:    
6:    freopen("input.txt", "r", stdin);  
7:    freopen("output.txt", "w", stdout);  
8:    
9:    scanf("%d", &N);  
10:    printf("%d", N);  
11:    return 0;  
12:  }

그리고, 아래와 같이 개발도구 (Visual Studio 2015 Desktop) 에서 볼 수 있도록 추가해줍니다.

아래와 같이 소스가 있는 Console.cpp 와 같은 폴더에 존재하면 간편합니다.

최종적으로는, Online Judge 사이트에 코드 제출시에는 해당 code 는 삭제가 되어야 합니다. 저는 보통 Console project 하나 만들어서 재활용하는데, 아래와 같이 처리하고 4 번 라인부터 제출하고 있습니다.

1:  #include "stdafx.h"  
2:  #define MY_LOCAL_TEST  
3:    
4:  #include <stdio.h>  
5:    
6:  int main(void) {  
7:    int N;  
8:    
9:  #ifdef MY_LOCAL_TEST  
10:    freopen("input.txt", "r", stdin);  
11:    freopen("output.txt", "w", stdout);  
12:  #endif  
13:    
14:    scanf("%d", &N);  
15:    printf("%d", N);

16:  #ifdef MY_LOCAL_TEST

17:    fclose(stdin);

18:    fclose(stdout);

19:  #endif 
20:    return 0;  
21:  }  
22:

추가1: freopen 에 대한 MSDN 내용

https://msdn.microsoft.com/ko-kr/library/wk2h68td.aspx

freopen() 에서 사용한 stdin, stdout 리소스에 대해서 fclose() 를 호출하는 것이 정석이고, stdin 만 사용하면 fclose 까지 사용하지 않아도 크게 문제되는 것은 없는 듯..

2016.12.21 추가 * Visual Studio 사용자면 그냥 아래 내용 참고
http://gooddaytocode.blogspot.kr/2016/06/visual-studio.html

* Compile 분기를 위한 define 은 ONLINE_JUDGE 를 쓰자.. 아래 내용 참고
http://gooddaytocode.blogspot.kr/search/label/%5B028%5D%20%EC%B1%84%EC%A0%90%20%EB%8F%84%EC%9B%80%EB%A7%90%EC%9D%84%20%EC%9D%BD%EC%96%B4%EB%B3%B4%EC%9E%90

2016년 4월 3일 일요일

알고리즘 시험 초보자를 위한 추천 읽을꺼리

알고리즘 시험 초보자를 위한 추천 읽을꺼리 3건입니다.

(1) 강의1 http://slides.com/gangseoklee/aps-5#/ (강의2 기반으로 작성된 것)

* 강의 추천 문제 링크: https://github.com/gangseok514/Note/wiki/Practice

(2) 강의2 http://slides.com/ilyoan/pscp#/

(3) ALGOSPOT 자주 하는 실수 모음

https://algospot.com/wiki/read/%EC%9E%90%EC%A3%BC_%ED%95%98%EB%8A%94_%EC%8B%A4%EC%88%98_%EB%AA%A8%EC%9D%8C

간단 정리 (위 링크의 소제목들입니다)

잘못된 알고리즘의 사용
테스트 케이스 여러 개가 한번에 입력될 때, 적절히 초기화하지 않는 문제
C 스타일 문자열에서 종결 문자를 고려하지 않고 배열 크기를 지정 (C/C++)
개행 문자 처리: 테스트 데이터 마지막줄에 '\n'가 없는 경우
변수 범위 오버플로우
cin/cout과 integer overflow
소수 처리
I/O 처리 속도
실수 출력
for(A; B; C)의 B에서 strlen 사용하기
STL에서 size()-1

알고리즘 문제해결 전략 [책]

몇 년째 읽는 책: 알고리즘 문제해결 전략
저자: 구종만
책 소개&코드: http://book.algospot.com/index.html

https://algospot.com 에서 문제 풀이를 할 수 있고,
책에 있는 코드는 알고리즘의 핵심부분만 존재하기 때문에
입출력은 직접 작성해야 합니다.

특정 주제를 공부하고, 예를 들어, 31 장 최소 스패닝 트리 관련 내용을 공부 후에 해당 코드를 기반으로 BOJ 의 알고리즘 분류 - 최소 스패닝 트리로 가서 문제를 골라서 풀어보면 됩니다. 코드 31.1 로 9372번: 상근이의 여행 (https://www.acmicpc.net/problem/9372) 은 쉽게 풀 수 있습니다.

문제해결을 위한 창의적 알고리즘 보다는 내용이 훨씬 어렵고,
2017 년 들어 수면용으로 잘 사용하고 있습니다. 2018 년도.. 그러고 있는 중이고, 2019 년에도.... ㅠ

1부 문제 해결 시작하기

1장 문제 해결과 프로그래밍 대회
- 1.1 도입
- 1.2 프로그래밍 대회
- 1.3 이 책을 읽는 방법
- 1.4 국내에서 참가할 수 있는 프로그래밍 대회들
- 1.5 대회 준비를 위한 조언
- 1.6 더 읽을 거리
2장 문제 해결 개관 (입문자 추천)
- 2.1 도입
- 2.2 문제 해결 과정
- 2.3 문제 해결 전략
- 2.4 더 읽을거리
3장 코딩과 디버깅에 관하여 (입문자 추천)
- 3.1 도입: 코딩의 중요성을 간과하지 말라
- 3.2 좋은 코드를 짜기 위한 원칙
- 3.3 자주 하는 실수
- 3.4 디버깅과 테스팅
- 3.5 변수 범위의 이해
- 3.6 실수 자료형의 이해(OPTIONAL)
- 3.7 더 읽을 거리

2부 알고리즘 분석

4장 알고리즘의 시간 복잡도 분석 (입문자 추천)
- 4.1 도입
- 4.2 선형 시간 알고리즘
- 4.3 선형 이하 시간 알고리즘
- 4.4 지수 시간 알고리즘
- 4.5 시간 복잡도
- 4.6 수행 시간 어림짐작하기
- 4.7 계산 복잡도 클래스: P, NP, NP-완비
- 4.8 더 읽을 거리
5장 알고리즘의 정당성 증명
- 5.1 도입
- 5.2 수학적 귀납법과 반복문 불변식
- 5.3 귀류법
- 5.4 다른 기술들
- 5.5 더 읽을 거리

3부 알고리즘 설계 패러다임

6장 무식하게 풀기 (입문자 추천)
- 6.1 도입
- 6.2 재귀 호출과 완전 탐색
- 6.3 문제: 소풍 (난이도: 하, 문제 ID: PICNIC)
- 6.4 풀이: 소풍
- 6.5 문제: 게임판 덮기 (난이도: 하, 문제 ID: BOARDCOVER)
- 6.6 풀이: 게임판 덮기
- 6.7 최적화 문제
- 6.8 문제: 시계 맞추기 (난이도: 중, 문제 ID: CLOCKSYNC)
- 6.9 풀이: 시계 맞추기
- 6.10 많이 등장하는 완전 탐색 유형
7장 분할 정복 (입문자 추천)
- 7.1 도입
- 7.2 문제: 쿼드 트리 뒤집기 (문제 ID: QUADTREE, 난이도: 하)
- 7.3 풀이: 쿼드 트리 뒤집기
- 7.4 문제: 울타리 잘라내기 (문제 ID: FENCE, 난이도: 중)
- 7.5 풀이: 울타리 잘라내기
- 7.6 문제: 팬 미팅 (문제 ID: FANMEETING, 난이도: 상)
- 7.7 풀이: 팬 미팅
8장 동적 계획법 (입문자 추천)
- 8.1 도입
- 8.2 문제: 와일드카드 (문제 ID: WILDCARD, 난이도: 중)
- 8.3 풀이: 와일드카드
- 8.4 전통적 최적화 문제들
- 8.5 문제: 합친 LIS (문제 ID: JLIS, 난이도: 하)
- 8.6 풀이: 합친 LIS
- 8.7 문제: 원주율 외우기 (문제 ID: PI, 난이도: 하)
- 8.8 풀이: 원주율 외우기
- 8.9 문제: QUANTIZATION (문제 ID: QUANTIZE, 난이도: 중)
- 8.10 풀이: QUANTIZATION
- 8.11 경우의 수와 확률
- 8.12 문제: 비대칭 타일링 (문제 ID: ASYMTILING, 난이도: 하)
- 8.13 풀이: 비대칭 타일링
- 8.14 문제: 폴리오미노 (문제 ID: POLY, 난이도: 중)
- 8.15 풀이: 폴리오미노
- 8.16 문제: 두니발 박사의 탈옥 (문제 ID: NUMB3RS, 난이도: 중)
- 8.17 풀이: 두니발 박사의 탈옥
9장 동적 계획법 테크닉
- 9.1 최적화 문제의 실제 답 계산하기
- 9.2 문제: 여행 짐 싸기 (문제 ID: PACKING, 난이도: 중)
- 9.3 풀이: 여행 짐 싸기
- 9.4 문제: 광학 문자 인식 (문제 ID: OCR, 난이도: 상)
- 9.5 풀이: 광학 문자 인식
- 9.6 K번째 답 계산하기
- 9.7 문제: K번째 최대 증가 부분 수열 (문제 ID: KLIS, 난이도: 상)
- 9.8 풀이: K번째 최대 증가 부분 수열
- 9.9 문제: 드래곤 커브 (문제 ID: DRAGON, 난이도: 중)
- 9.10 풀이: 드래곤 커브
- 9.11 정수 이외의 입력에 대한 메모이제이션
- 9.12 문제: 웨브바짐 (문제 ID: ZIMBABWE, 난이도: 상)
- 9.13 풀이: 웨브바짐
- 9.14 문제: 실험 데이터 복구하기 (문제 ID: RESTORE, 난이도: 중)
- 9.15 풀이: 실험 데이터 복구하기
- 9.16 조합 게임
- 9.17 문제: 숫자 게임 (문제 ID: NUMBERGAME, 난이도: 하)
- 9.18 풀이: 숫자 게임
- 9.19 문제: 블록 게임 (문제 ID: BLOCKGAME, 난이도: 중)
- 9.20 풀이: 블록 게임
- 9.21 반복적 동적 계획법
- 9.22 문제: 회전초밥 (문제 ID: SUSHI, 난이도: 중)
- 9.23 풀이: 회전초밥
- 9.24 문제: 지니어스 (문제 ID: GENIUS, 난이도: 중)
- 9.25 풀이: 지니어스
- 9.26 더 읽을 거리
10장 탐욕법
- 10.1 도입
- 10.2 문제: 도시락 데우기 (문제 ID: LUNCHBOX, 난이도: 하)
- 10.3 풀이: 도시락 데우기
- 10.4 문제: 문자열 합치기 (문제 ID: STRJOIN, 난이도: 중)
- 10.5 풀이: 문자열 합치기
- 10.6 문제: 미나스 아노르 (문제 ID: MINASTIRITH, 난이도: 상)
- 10.7 풀이: 미나스 아노르
11장 조합 탐색
- 11.1 도입
- 11.2 조합 탐색 기법들
- 11.3 문제: 게임판 덮기 2 (문제 ID: BOARDCOVER2, 난이도: 하)
- 11.4 풀이: 게임판 덮기 2
- 11.5 문제: 알러지가 심한 친구들 (문제 ID: ALLERGY, 난이도: 중)
- 11.6 풀이: 알러지가 심한 친구들
- 11.7 문제: 카쿠로 (문제 ID: KAKURO2, 난이도: 중)
- 11.8 풀이: 카쿠로
- 11.9 더 읽을거리
12장 최적화 문제 결정 문제로 바꿔 풀기
- 12.1 도입
- 12.2 문제: 남극 기지 (문제 ID: ARCTIC, 난이도: 하)
- 12.3 풀이: 남극 기지
- 12.4 문제: 캐나다 여행 (문제 ID: CANADATRIP, 난이도: 중)
- 12.5 풀이: 캐나다 여행
- 12.6 문제: 수강 철회 (문제 ID: WITHDRAWAL, 난이도: 상)
- 12.7 풀이: 수강 철회

4부 유명한 알고리즘들

13장 수치 해석
- 13.1 도입
- 13.2 이분법
- 13.3 문제: 승률 올리기 (문제 ID: RATIO, 난이도: 하)
- 13.4 풀이: 승률 올리기
- 13.5 삼분 검색
- 13.6 문제: 꽃가루 화석 (문제 ID: FOSSIL, 난이도: 상)
- 13.7 풀이: 꽃가루 화석
- 13.8 다른 주제들
14장 정수론
- 14.1 도입
- 14.2 소수
- 14.3 문제: 비밀번호 486 (문제 ID: PASS486, 난이도: 중)
- 14.4 풀이: 비밀번호 486
- 14.5 유클리드 알고리즘
- 14.6 문제: 마법의 약 (문제 ID: POTION, 난이도: 중)
- 14.7 풀이: 마법의 약
- 14.8 모듈라 연산
- 14.9 더 읽을거리(OPTIONAL)
15장 계산 기하
- 15.1 도입
- 15.2 계산 기하의 도구들
- 15.3 교차와 거리, 면적
- 15.4 문제: 핀볼 시뮬레이션 (문제 ID: PINBALL, 난이도: 상)
- 15.5 풀이: 핀볼 시뮬레이션
- 15.6 다각형
- 15.7 문제: 보물섬 (문제 ID: TREASURE, 난이도: 상)
- 15.8 풀이: 보물섬
- 15.9 문제: 너드인가, 너드가 아닌가? (문제 ID: NERDS, 난이도: 중)
- 15.10 풀이: 너드인가, 너드가 아닌가?
- 15.11 계산 기하 알고리즘 디자인 패턴
- 15.12 자주 하는 실수와 유의점들
- 15.13 더 읽을거리

5부 기초 자료 구조

16장 비트마스크
- 16.1 도입
- 16.2 비트마스크를 이용한 집합의 구현
- 16.3 비트마스크의 응용 예제
- 16.4 문제: 졸업 학기 (문제 ID: GRADUATION, 난이도: 중)
- 16.5 풀이: 졸업 학기
- 16.6 더 읽을거리
17장 부분 합
- 17.1 도입
- 17.2 문제: 크리스마스 인형 (문제 ID: CHRISTMAS, 난이도: 중)
- 17.3 풀이: 크리스마스 인형
- 17.4 더 공부할 거리
18장 선형 자료 구조 (입문자 추천)
- 18.1 도입
- 18.2 동적 배열
- 18.3 연결 리스트
- 18.4 동적 배열과 연결 리스트의 비교
- 18.5 문제: 조세푸스 문제 (문제 ID: JOSEPHUS, 난이도: 하)
- 18.6 풀이: 조세푸스 문제
- 18.7 더 읽을 거리
19장 큐와 스택, 데크 (입문자 추천)
- 19.1 도입
- 19.2 큐와 스택, 데크의 구현
- 19.3 스택과 큐의 활용
- 19.4 문제: 짝이 맞지 않는 괄호 (문제 ID: BRACKETS2, 난이도: 하)
- 19.5 풀이: 짝이 맞지 않는 괄호
- 19.6 문제: 외계 신호 분석 (문제 ID: ITES, 난이도: 중)
- 19.7 풀이: 외계 신호 분석
20장 문자열
- 20.1 도입
- 20.2 문자열 검색
- 20.3 문제: 재하의 금고 (문제 ID: JAEHASAFE, 난이도: 중)
- 20.4 풀이: 재하의 금고
- 20.5 접미사 배열
- 20.6 문제: 말버릇 (문제 ID: HABIT, 난이도: 중)
- 20.7 풀이: 말버릇
- 20.8 더 읽을거리

6부 트리

21장 트리의 구현과 순회 (입문자 추천)
- 21.1 도입
- 21.2 트리의 순회
- 21.3 문제: 트리 순회 순서 변경 (문제 ID: TRAVERSAL, 난이도: 하)
- 21.4 풀이: 트리 순회 순서 변경
- 21.5 문제: 요새 (문제 ID: FORTRESS, 난이도: 중)
- 21.6 풀이: 요새
22장 이진 검색 트리 (입문자 추천)
- 22.1 도입
- 22.2 이진 검색 트리의 정의와 조작
- 22.3 시간 복잡도 분석과 균형 잡힌 이진 검색 트리
- 22.4 문제: 너드인가, 너드가 아닌가? 2 (문제 ID: NERD2, 난이도: 중)
- 22.5 풀이: 너드인가, 너드가 아닌가? 2
- 22.6 균형 잡힌 이진 검색 트리 직접 구현하기: 트립
- 22.7 문제: 삽입 정렬 뒤집기 (문제 ID: INSERTION, 난이도: 중)
- 22.8 풀이: 삽입 정렬 뒤집기
23장 우선순위 큐와 힙 (입문자 추천)
- 23.1 도입
- 23.2 힙의 정의와 구현
- 23.3 문제: 변화하는 중간 값 (문제 ID: RUNNINGMEDIAN, 난이도: 하)
- 23.4 풀이: 변화하는 중간 값
24장 구간 트리
- 24.1 구간 트리: 구간에 대한 질문 대답하기
- 24.2 문제: 등산로 (문제 ID: MORDOR, 난이도: 중)
- 24.3 풀이: 등산로
- 24.4 문제: 족보 탐험 (문제 ID: FAMILYTREE, 난이도: 상)
- 24.5 풀이: 족보 탐험
- 24.6 펜윅 트리: 빠르고 간단한 구간 합
- 24.7 문제: 삽입 정렬 시간 재기 (문제 ID: MEASURETIME, 난이도: 중)
- 24.8 풀이: 삽입 정렬 시간 재기
25장 상호 배타적 집합
- 25.1 도입
- 25.2 문제: 에디터 전쟁 (문제 ID: EDITORWARS, 난이도: 중)
- 25.3 풀이: 에디터 전쟁
26장 트라이
- 26.1 도입
- 26.2 문제: 안녕히, 그리고 물고기는 고마웠어요! (문제 ID: SOLONG, 난이도: 중)
- 26.3 풀이: 안녕히, 그리고 물고기는 고마웠어요!
- 26.4 트라이를 이용한 다중 문자열 검색
- 26.5 문제: 보안종결자 (문제 ID: NH, 난이도: 상)
- 26.6 풀이: 보안종결자

7부 그래프

27장 그래프의 표현과 정의 (입문자 추천)
- 27.1 도입
- 27.2 그래프의 사용 예
- 27.3 암시적 그래프 구조들
- 27.4 그래프의 표현 방법
28장 그래프의 깊이 우선 탐색 (입문자 추천)
- 28.1 도입
- 28.2 문제: 고대어 사전 (문제 ID: DICTIONARY, 난이도: 하)
- 28.3 풀이: 고대어 사전
- 28.4 오일러 서킷
- 28.5 문제: 단어 제한 끝말잇기 (문제 ID: WORDCHAIN, 난이도: 하)
- 28.6 풀이: 단어 제한 끝말잇기
- 28.7 이론적 배경과 응용
- 28.8 문제: 감시 카메라 설치 (문제 ID: GALLERY, 난이도: 중)
- 28.9 풀이: 감시 카메라 설치
- 28.10 문제: 회의실 배정 (문제 ID: MEETINGROOM, 난이도: 상)
- 28.11 풀이: 회의실 배정
29장 그래프의 너비 우선 탐색 (입문자 추천)
- 29.1 도입
- 29.2 문제: SORTING GAME (문제 ID: SORTGAME, 난이도: 중)
- 29.3 풀이: SORTING GAME
- 29.4 문제: 어린이날 (문제 ID: CHILDRENDAY, 난이도: 상)
- 29.5 풀이: 어린이날
- 29.6 최단 경로 전략
- 29.7 문제: 하노이의 탑 (문제 ID: HANOI4B, 난이도: 중)
- 29.8 풀이: 하노이의 탑
30장 최단 경로 알고리즘 (입문자 추천)
- 30.1 도입
- 30.2 다익스트라의 최단 경로 알고리즘
- 30.3 문제: 신호 라우팅 (문제 ID: ROUTING, 난이도: 하)
- 30.4 풀이: 신호 라우팅
- 30.5 문제: 소방차 (문제 ID: FIRETRUCKS, 난이도: 중)
- 30.6 풀이: 소방차
- 30.7 문제: 철인 N종 경기 (문제 ID: NTHLON, 난이도: 상)
- 30.8 풀이: 철인 N종 경기
- 30.9 벨만-포드의 최단 경로 알고리즘
- 30.10 문제: 시간여행 (문제 ID: TIMETRIP, 난이도: 중)
- 30.11 풀이: 시간여행
- 30.12 플로이드의 모든 쌍 최단 거리 알고리즘
- 30.13 문제: 음주 운전 단속 (문제 ID: DRUNKEN, 난이도: 중)
- 30.14 풀이: 음주 운전 단속
- 30.15 문제: 선거 공약 (문제 ID: PROMISES, 난이도: 중)
- 30.16 풀이: 선거 공약
31장 최소 스패닝 트리
- 31.1 도입
- 31.2 크루스칼의 최소 스패닝 트리 알고리즘
- 31.3 프림의 최소 스패닝 트리 알고리즘
- 31.4 문제: 근거리 네트워크 (문제 ID: LAN, 난이도: 하)
- 31.5 풀이: 근거리 네트워크
- 31.6 문제: 여행 경로 정하기 (문제 ID: TPATH, 난이도: 상)
- 31.7 풀이: 여행 경로 정하기
32장 네트워크 유량